Selectividad Andalucía 2018 Septiembre A2
SOLUCIÓN
– b) ¿En qué intervalo de tiempo decrece el consumo de cereales?
Estudiamos la monotonía (crecimiento y decrecimiento)
![]()
![]()
![]()
Resolvemos la ecuación de segundo grado
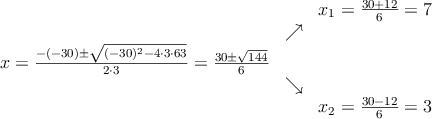
Las soluciones nos dividen la recta en tres intervalos
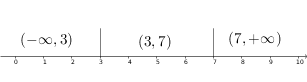
Comprobamos en cada intervalo si la función crece o decrece (tomando un punto de cada intervalo y verificando el signo de la derivada)
![]() CRECE
CRECE
![]() DECRECE
DECRECE
![]() CRECE
CRECE

Por tanto entre t=3 y t=7 decrece el consumo de cereales
– a) ¿En qué instante se alcanza el máximo consumo de cereales y cuántas toneladas se consumen en ese momento?
Dado que es una función continua (por ser polinómica), el estudio de la monotonía del apartado anterior nos dice que tiene un máximo en t=3
Además debemos comprobar también los puntos de los extremos del intervalo: 0 y 12
– ![]()
– ![]()
– ![]()
Luego para t=12 se obtiene el máximo consumo de cerales: 334000 toneladas
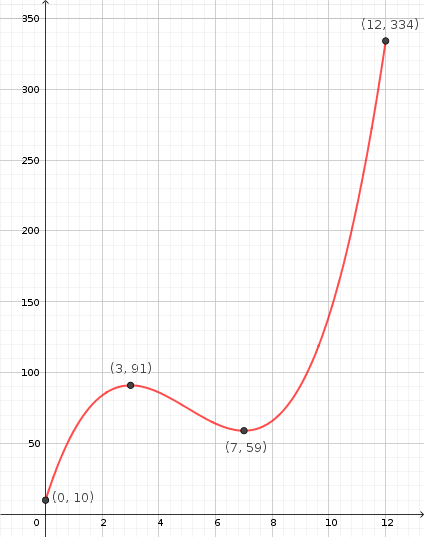
Representación gráfica