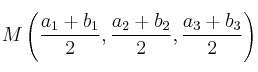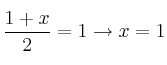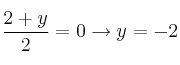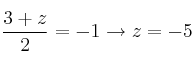09 - Simétrico de un punto respecto de otro punto
4 - DISTANCIAS, ÁNGULOS y SIMETRÍAS
 01 - Distancia entre dos puntos
01 - Distancia entre dos puntos 02 - Distancia de un punto a un plano
02 - Distancia de un punto a un plano 03 - Distancia de un punto a una recta
03 - Distancia de un punto a una recta 04 - Distancia entre rectas que se cruzan
04 - Distancia entre rectas que se cruzan 05 - Ángulo entre dos vectores
05 - Ángulo entre dos vectores 06 - Ángulo entre dos rectas
06 - Ángulo entre dos rectas 07 - Ángulo entre dos planos
07 - Ángulo entre dos planos 08 - Ángulo entre recta y plano
08 - Ángulo entre recta y plano 09 - Simétrico de un punto respecto de otro punto
09 - Simétrico de un punto respecto de otro punto 10 - Simétrico de un punto respecto de una recta
10 - Simétrico de un punto respecto de una recta 11 - Simétrico de un punto respecto de un plano
11 - Simétrico de un punto respecto de un plano