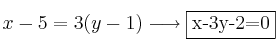Ecuación de la mediana
SOLUCIÓN
La mediana correspondiente al vértice ![]() es la recta que une
es la recta que une ![]() con el punto medio del segemento
con el punto medio del segemento ![]()
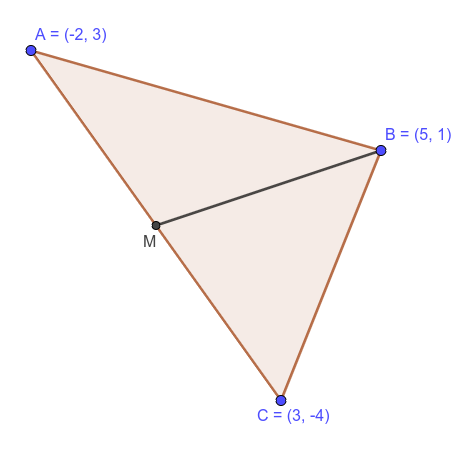
Hallamos el punto medio del segmento ![]() , al que llamamos
, al que llamamos ![]()
Recuerda como hallar el punto medio de un segmento
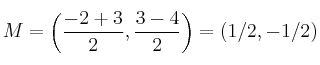
Ahora tan sólo nos queda crear la recta que pasa por ![]() y
y ![]()
Como punto tomamos ![]() y como vector
y como vector 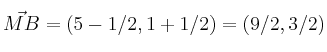
También nos vale cualquier otro vector proporcional, por ejemplo ![]() , o incluso
, o incluso ![]()
La mediana en ec. continua sería:
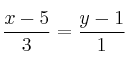
Si queremos expresarla en ecuación general: