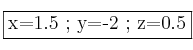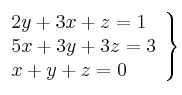sistemas ecuaciones lineal 3x3
SOLUCIÓN
Para resolver el sistema podemos usar varios métodos (gauss, sustitución, etc.).
Usaremos el método de sustitución.
Despejaremos "z" en la primera ecuación
![]()
La expresión obtenida la sustituimos por "z" en las demás ecuaciones:
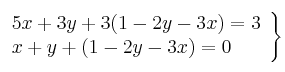
Nos ha quedado un sistema de 2 ecuaciones con 2 incógnitas.
Quitamos paréntesis, ordenamos las ecuaciones y resolvemos el sistema.
Obtenemos como soluciones ![]() y
y ![]()
Ahora nos vamos a la expresión donde teníamos z despejada:
![]() y sustituimos x e y por sus valores
y sustituimos x e y por sus valores
![]()
![]()
Las soluciones son: