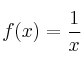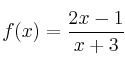Calcular dominio de una función 4081
SOLUCIÓN
– a) ![]()
– b) ![]() (por ser polinómica)
(por ser polinómica)
– c) ![]() (por ser polinómica)
(por ser polinómica)
– d) ![]()
– e) 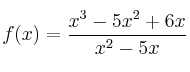
El dominio de una función racional es todo R excepto los valores que anulan el denominador. Para calcularlos igualamos el denominador a cero:
![]() Las soluciones de la ecuación anterior son
Las soluciones de la ecuación anterior son ![]() y
y ![]() . Por tanto el dominio es:
. Por tanto el dominio es:
![]()
– f) 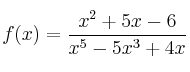
El dominio de una función racional es todo R excepto los valores que anulan el denominador. Para calcularlos igualamos el denominador a cero:
![]() Las soluciones de la ecuación anterior son
Las soluciones de la ecuación anterior son ![]() ;
; ![]() ,
, ![]() ;
; ![]() ;
; ![]() . Por tanto el dominio es:
. Por tanto el dominio es:
![]()
– g) ![]() (por ser exponencial)
(por ser exponencial)
– h) ![]()
![]()
![]()
– i) ![]()
![]()
![]()
– j) ![f(x) = \sqrt[4]{x^2-5x+6} f(x) = \sqrt[4]{x^2-5x+6}](local/cache-vignettes/L183xH50/e9e191119e0249588b43a43827057666-138b1.png?1688084123)
Se trata de una función irracional (con raíz par). El dominio son todos los números que verifiquen que el radicando sea mayor o igual que cero
![]()
Estamos ante una inecuación de segundo grado. Para resolverla podemos representar la parábola ![]() y ver qué valores están por encima del eje horizontal. Obtendremos como solución
y ver qué valores están por encima del eje horizontal. Obtendremos como solución ![]() . Por tanto el dominio es:
. Por tanto el dominio es:
![]()