Contraste Bilateral Media

|

Los depósitos mensuales, en euros, en una entidad bancaria siguen una distribución normal de media $\mu$ y desviación típica $\sigma = 5.1$ . Con el fin de contrastar si la media de los depósitos mensuales es 20 €, se toma una muestra de tamaño 16, y la media muestral resulta ser 22.4 €. ¿Se puede aceptar la hipótesis de que la media es 20 € a un nivel de significación del $5\%$ ?

SOLUCIÓN

Se trata de un contraste de hipótesis bilateral para la media (ver la teoría).

Contraste
$H_0: \mu = 20$ (la media de los depósitos es de 20 €)
$H_1: \mu \neq 20$ (la media de los depósitos es distinta de 20 €))

Datos
$\sigma = 5.1$

$\overline{x}=22.4$
confianza: $95 \% \Rightarrow z_c=1.96$

Región de aceptación (R)

$R = \left( k-Z_c \cdot \frac{\sigma}{\sqrt{n}}, k+Z_c \cdot \frac{\sigma}{\sqrt{n}}\right)$

$R = \left( 20-1.96 \cdot \frac{5.1}{\sqrt{16}}, 20+1.96 \cdot \frac{5.1}{\sqrt{16}}\right)$

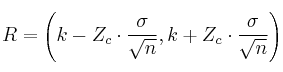
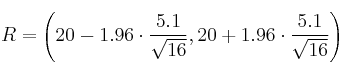
Decisión:
Como $22.4 \in (17.501, 22.449) \Rightarrow$ Aceptamos

Podemos afirmar que la media de depósitos mensuales es de 20 € (con un nivel de significación de 0.05)

Palabras clave