Contraste Unilateral Proporción
SOLUCIÓN
Contraste unilateral para la proporción (Ver Teoría)
![]() (hipótesis nula: proporción de fumadores
(hipótesis nula: proporción de fumadores ![]() )
)
![]() (hipótesis alternativa: proporción de fumadores
(hipótesis alternativa: proporción de fumadores ![]() )
)
Datos del problema
![]()
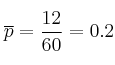
![]() (confianza del
(confianza del ![]() )
)
Región de aceptación (R)
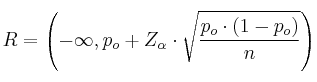
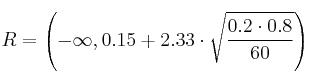
![]()
Toma de decisión
![]() Aceptamos
Aceptamos ![]()
Es cierta la afirmación del profesor con un nivel de significación de 0.01
– b) Para un nivel de confianza del ![]() ,
, ![]() , entonces la región de aceptación sería (cambiando 2.33 por 1.28):
, entonces la región de aceptación sería (cambiando 2.33 por 1.28):
![]()
Por lo que también aceptaríamos la hipótesis nula a un nivel de confianza es del
