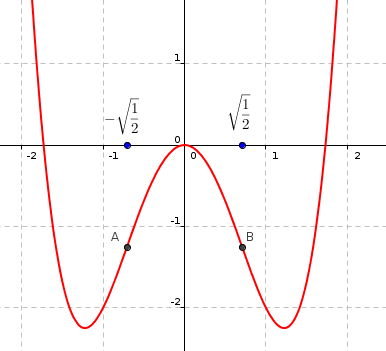
Curvatura y puntos de inflexión

| 2 |

Estudia la curvatura y puntos de inflexión de la función f(x)=x^4-3x^2

SOLUCIÓN

f^\prime(x)=4x^3-6x
f^{\prime \prime}(x)=12x^2-6
f^{\prime \prime\prime}(x)=24x

f^{\prime \prime}(x)=0 \longrightarrow 12x^2-6=0 \longrightarrow x=\pm \sqrt{\frac{1}{2}}

Los intervalos a considerar son: 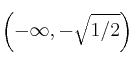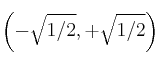\left(-\infty, -\sqrt{1/2}\right) ; \left(-\sqrt{1/2}, +\sqrt{1/2}\right) y \left(+\sqrt{1/2}, +\infty\right).

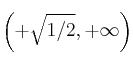Del primer intervalo tomamos, por ejemplo x=-3
f^{\prime \prime}(-3) = 12 \cdot (-3)^2 -6 = 102 >0 \Longrightarrow f convexa en \left(-\infty, -\sqrt{1/2}\right)

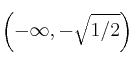
Del segundo intervalo tomamos, por ejemplo x=0
f^{\prime \prime}(0) = 12 \cdot (0)^2 -6 = -6 <0 \Longrightarrow f cóncava en \left(-\sqrt{1/2}, +\sqrt{1/2}\right)

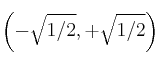
Del tercer intervalo tomamos, por ejemplo x=3
f^{\prime \prime}(3) = 12 \cdot (3)^2 -6 = 102 >0 \Longrightarrow f convexa en \left(+\sqrt{1/2}, +\infty\right)

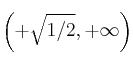
Para los puntos de inflexión tenemos, como candidatos, los puntos donde se anula la segunda derivada: 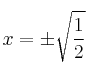x=\pm \sqrt{\frac{1}{2}}. Le aplicamos la 3ª derivada:

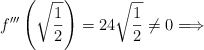– f^{\prime \prime\prime}\left(\sqrt{\frac{1}{2}}\right) = 24 \sqrt{\frac{1}{2}} \neq 0 \Longrightarrow es punto de inflexión.
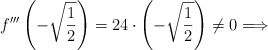– f^{\prime \prime\prime}\left(-\sqrt{\frac{1}{2}}\right) = 24 \cdot \left(-\sqrt{\frac{1}{2}}\right) \neq 0 \Longrightarrow es punto de inflexión.
Ambos son puntos de inflexión. Si nos pidiesen la segunda coordenada de esos puntos de inflexión usaríamos la función original (sustituyendo x por el punto).

La gráfica de la función sería: