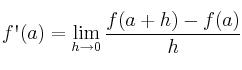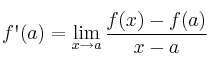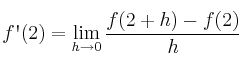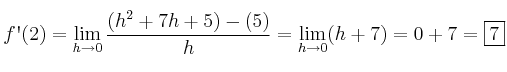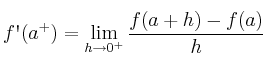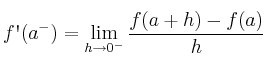Derivada de una función en un punto
Dada una funcion 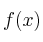 , llamamos derivada de
, llamamos derivada de 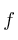 en el punto
en el punto 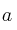 , y lo representamos por
, y lo representamos por 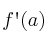 a a siguiente expresión:
a a siguiente expresión:
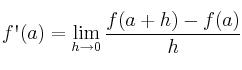
También se puede usar la siguiente expresión equivalente:
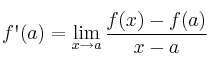
Ejemplo: Calcula la derivada en el punto 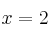 de la función
de la función 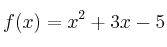
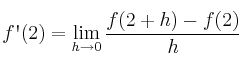
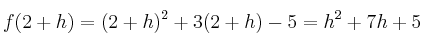
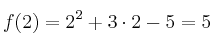
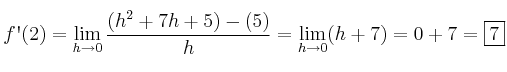
Afortunadamente no siempre tendremos que usar límites, pues en la mayoría de ocasiones calcularemos las derivadas usando las fórmulas
Derivadas laterales
La derivada, por definición es un límite, y al igual que existen límites laterales, también existen derivadas laterales:
– Derivada por la derecha: 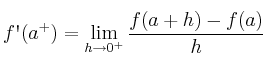
– Derivada por la izquierda: 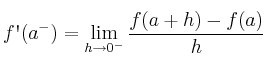
Tendremos que usar las derivadas laterales en las funciones a trozos.
 Definición de Derivada
Definición de Derivada Interpretación geométrica de la derivada
Interpretación geométrica de la derivada Resumen de fórmulas (derivadas)
Resumen de fórmulas (derivadas) Monotonía (crecimiento-decrecimiento) de una función
Monotonía (crecimiento-decrecimiento) de una función Extremos (máximos y mínimos) de una función
Extremos (máximos y mínimos) de una función Curvatura (concavidad y convexidad) y puntos de inflexión
Curvatura (concavidad y convexidad) y puntos de inflexión Regla de l’Hôpital (I)
Regla de l’Hôpital (I) L’Hôpital (II) : indeterminación 0 · infinito
L’Hôpital (II) : indeterminación 0 · infinito L’Hôpital (III) : indeterminación infinito elevado a cero
L’Hôpital (III) : indeterminación infinito elevado a cero