Desarrollo de un determinante por los elementos de una línea

| 1 |

Desarrollo de un determinante por los elementos de una línea

- Podemos calcular un determinante, de cualquier orden, desarrollándolo por los elementos de una línea (fila o columna).
- Usaremos este método para determinantes de orden 4 o superior.
- También podemos usarlo para determinantes de orden 3 (aunque en este caso tenemos como alternativa la Regla de Sarrus.

- El método se basa en la siguiente propiedad: «Un determinante es igual a la suma de los elementos de una línea multiplicados por sus adjuntos».
- Podemos desarrollarlo por la fila o columna que elijamos. En la práctica se elige la línea que contenga más ceros (para hacer menos cálculos)

Ejemplo: Desarrollamos un det. por los elementos de la primera fila

\left| \begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array} \right| = a_{11} \cdot A_{11} + a_{12} \cdot A_{12} + a_{13} \cdot A_{13}

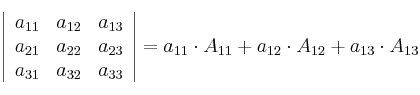
Ejemplo numérico:

\left| \begin{array}{ccc} 0 & 1 & 2 \\ 3 & 4 & 5 \\ 6 & 7 & 8 \end{array} \right| = 0 \cdot \left| \begin{array}{cc} 4 & 5 \\ 7 & 8 \end{array} \right| - 1 \cdot \left| \begin{array}{cc} 3 & 5 \\ 6 & 8 \end{array} \right| + 2 \cdot \left| \begin{array}{cc} 3 & 4 \\ 6 & 7 \end{array} \right| =
0 - 1\cdot(-6) + 2 \cdot (-3) = 0

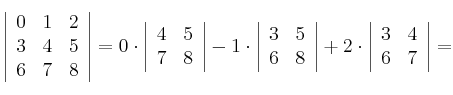
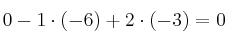
NOTA: Hemos cambiado el signo del segundo sumando porque 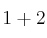1+2 es impar.

Puedes calcular cualquier determinante de orden 3 en el siguiente enlace:
Calcular determinante online