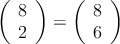Una variable aleatoria sigue una binomial si:
1) Hay un experimento aleatorio que se repite 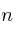 veces con independencia (ejemplo: lanzar una moneda 100 veces)
veces con independencia (ejemplo: lanzar una moneda 100 veces)
2) En cada prueba solo pueden darse dos casos: éxito o fracaso (ejemplo: cara o cruz). Las probabilidades de ambos suman uno pero no tienen que ser la misma.
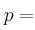 probabilidad de obtener éxito
probabilidad de obtener éxito
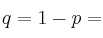 probabilidad de no obtener éxito (fracaso)
probabilidad de no obtener éxito (fracaso)
3) La variable se define como el número de éxitos conseguidos:
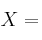 número de éxitos conseguidos en los
número de éxitos conseguidos en los 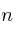 experimentos.
experimentos.
Para simplificar, lo expresamos de la siguiente manera:
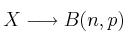
Su función de probabilidad es la siguiente:
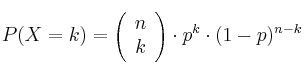
para
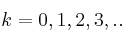
Su media o Esperanza Matemática (valor esperado) es 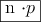
La expresión 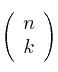 se llama número combinatorio y se lee «n sobre k»
se llama número combinatorio y se lee «n sobre k»
Para calcularlo se usa la siguiente fórmula:
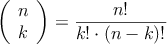
Ejemplo:
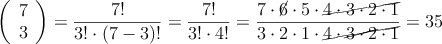
Algunas propiedades de los números combinatorios
– 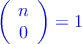 Ejemplo:
Ejemplo: 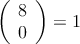
– 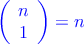 Ejemplo:
Ejemplo: 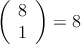
– 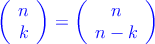 Ejemplo:
Ejemplo: