Distribución Muestral de Medias

|

Dada una distribución de probabilidad X=\{ x_1,x_2, .. \}, si extraemos muestras de tamaño n y calculamos la media (\overline{x}_i) de cada una de las muestras, podemos construir otra distribución con estos valores de las medias:
\overline{X}=\{ \overline{x}_1, \overline{x}_2, .. \}
a la que llamaremos Distribución Muestral de Medias y denotaremos por \overline{X}

La Distribución Muestral de Medias cumple el siguiente teorema:

Si la variable aleatoria X sigue una distribución de media \mu y desviación típica \sigma

X \longrightarrow ?(\mu, \sigma)


entonces se cumple que:
La Distribución Muestral de Medias \overline{X} sigue una distribución normal de media \mu y desviación típica \frac{\sigma}{\sqrt{n}}

\overline{X} \longrightarrow N \left( \mu, \frac{\sigma}{\sqrt{n}} \right)


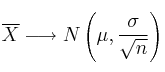
siempre que ocurra alguna de las dos condiciones siguientes:
– n \geq 30
– X \longrightarrow N (sea una distribución normal)

Ejemplo en vídeo: