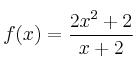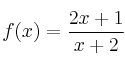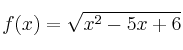Dominio y corte con los ejes
SOLUCIÓN
Dominio:
– a) ![]()
– b) ![]()
– c) ![]()
– d) No existe logaritmo de números negativos ni de cero, por tanto 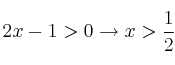
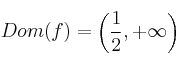
– e) No existe raíz cuadrada de números negativos, por tanto ![]() . Es una inecuación de segundo grado. Su solución será el dominio de la función.
. Es una inecuación de segundo grado. Su solución será el dominio de la función.
![]()
(Ver vídeos sobre [inecuaciones->http://matematicasies.com/-Inecuaciones-)
Corte con los ejes
– a) ![]() . Punto de corte
. Punto de corte ![]()
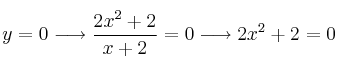 Ecuación de 2º grado que no tiene solución, por tanto ya no hay más puntos de corte.
Ecuación de 2º grado que no tiene solución, por tanto ya no hay más puntos de corte.
– b) ![]() . Punto de corte
. Punto de corte ![]()
![]() Ecuación de 2º grado que tiene como soluciones
Ecuación de 2º grado que tiene como soluciones ![]() y
y ![]() , por tanto, los puntos de corte son
, por tanto, los puntos de corte son ![]() y
y ![]()
– c) ![]() . Punto de corte
. Punto de corte ![]()
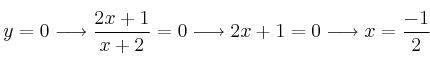 Punto de corte:
Punto de corte: ![]() .
.
– d) ![]() . No hay logaritmos de números negativos, por tanto no hay puntos de corte en el eje OY.
. No hay logaritmos de números negativos, por tanto no hay puntos de corte en el eje OY.
![]() (pues
(pues ![]() )
) ![]() Punto de corte:
Punto de corte: ![]() .
.
– e) 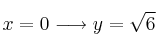 . Punto de corte:
. Punto de corte: 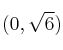 .
.
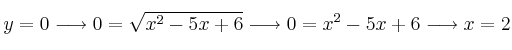 y
y ![]() . Puntos de corte:
. Puntos de corte: ![]() y
y ![]() .
.