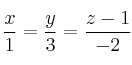Ejercicio planos y rectas en el espacio

|

Dados los puntos A(1,2,3), B(1,0,0) y C(0,1,1), se pide:

– a) Ecuación del plano \pi que pasa por A, B y C
– b) Vector normal al plano \pi
– c) Ecuación de una recta perpendicular al plano \pi y que pase por el punto (0,0,1)

SOLUCIÓN

– a) Un plano se puede determinar con un punto y dos vectores.
Punto: A(1,2,3)
Vectores 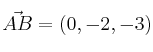\vec{AB}=(0,-2,-3) y \vec{AC}=(-1,-1,1)

\left| \begin{array}{ccc} x-1 & y-2 & z-3 \\ 0 & -2 & -3 \\ -1 & -1 & -2 \end{array} \right| = 0

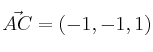
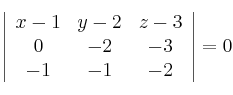
Resolvemos el determinante y obtenemos la ecuación del plano:
x+3y-2z-1=0

– b) De la ecuación anterior obtenemos el vector normal (1,3,-2)

– c) Para determinar una recta necesitamos vector y punto.
El punto nos lo da el enunciado: (0,0,1)
Una recta perpendicular a un plano, tiene como vector director el vector normal al plano, en este caso: (1,3,-2)

Por tanto, una ecuación de la recta sería:

\frac{x}{1}=\frac{y}{3}=\frac{z-1}{-2}