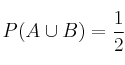Ejercicios Probabilidad
SOLUCIÓN
– a) Sabemos que:
A y B independientes ![]()
![]()
Debemos calcular ![]() , para ello usamos la fórmula de la unión
, para ello usamos la fórmula de la unión
![]()
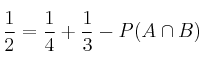
Ya podemos despejar ![]() obteniendo
obteniendo 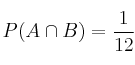
Ahora estamos en condiciones de comprobar la independencia:
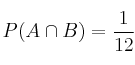
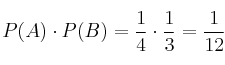
Como ![]() entonces
entonces ![]() y
y ![]() son independientes
son independientes
– b) 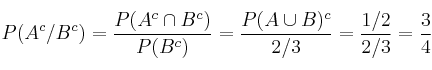
En el primer paso hemos aplicado la fórmula de la Probabilidad Condicionada, y en el segundo paso hemos aplicado en el numerador las Leyes de Morgan

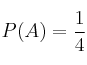 ,
, 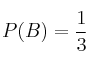 y
y