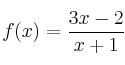Funciones gráfica

|

Represente gráficamente la siguiente función:

f(x) = \frac{3x-2}{x+1}

Indica dominio, monotonía y asíntotas

SOLUCIÓN

Dom(f) = R - \{-1\}

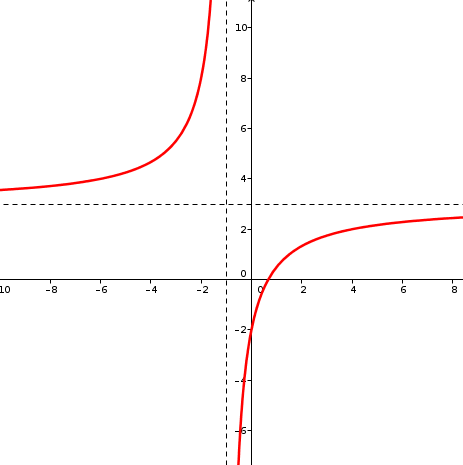
Asíntota vertical: 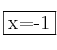\fbox{x=-1}
Asíntota horizontal: 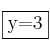\fbox{y=3}

Monotonía. Se trataa de un hipérbola (son siempre crecientes o siempre decrecientes).
Hacemos el estudio de la monotonía mediante el signo de la derivada primera:
f’(x) = \frac{5}{(x+1)^2}
La ecuación f’(x) = \frac{5}{(x+1)^2} =0 no tiene ninguna solución.
Para construir los intervalos (de crecimiento y decrecimiento), además de las soluciones de la ecuación anterior, se usan los puntos de corte o discontinuidad (en nuestro caso x=-1), por tanto los intervalos serían:
(-\infty,-1) y (-1,+\infty)

Podemos observar que la derivada f’(x) = \frac{5}{(x+1)^2} es siempre positiva (el numerador es positivo y el denominador es un cuadrado, por tanto también positivo).
La función es creciente en ambos intervalos, al ser siempre la derivada positiva.

La gráfica de la función es la siguiente: