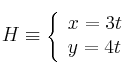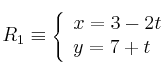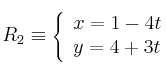Hallar paralela y perpendicular
SOLUCIÓN
Al ser paralela, tiene la misma dirección (el mismo vector director). Con el vector director y el punto que nos dan, tenemos la recta.
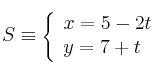
La recta ![]() tiene como vector director
tiene como vector director ![]() . Para conseguir una perpendicular, necesitamos un vector perpendicular al
. Para conseguir una perpendicular, necesitamos un vector perpendicular al ![]() , que sería el
, que sería el ![]() .
.
Con el vector ![]() y el punto que nos dan
y el punto que nos dan ![]() , ya tenemos la recta:
, ya tenemos la recta: