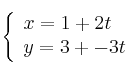Hallar recta perpendicular
SOLUCIÓN
Para expresar las ecuaciones de una recta necesitamos un punto y un vector director.
El punto nos lo proporciona el enunciado: 
El vector debe ser un vector perpendicular al vector director de 
Necesitamos hallar el vector director de la recta y encontrar otro perpendicular.
Hay varios procedimientos y fórmulas para obtener un vector director de la recta . El que usaremos en este ejercicio consiste en obtener dos puntos de la recta y, a partir de ellos, generar el vector.
Si 
entonces 
de donde 
. Punto1 
Si 
entonces 
de donde 
. Punto2 
Vector: 
.
Vector perpendicular : 
Con el punto y el vector expresamos las ecuaciones paramétricas de la recta que nos piden:
