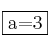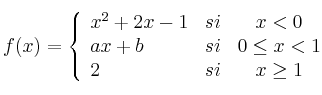Hallar valores que hagan continua la función

|

Halla los valores de a y b para que la siguiente función sea continua:

f(x)= \left\{ \begin{array}{lcc} x^2+2x-1 & si & x < 0 \\ ax+b & si & 0 \leq x < 1 \\ 2 & si & x \geq 1 \end{array} \right.

SOLUCIÓN

En (-\infty, 0) es continua por ser polinómica
En (0, 1) es continua por ser polinómica
En (1, +\infty) es continua por ser polinómica

Estudiamos la continuidad en los puntos que separan los trozos:

Veamos en x=0
– f(0) = a \cdot 0 + b = b
– \lim_{x \rightarrow 0^-} f(x) =\lim_{x \rightarrow 0} (x^2+2x-1) = -1
– \lim_{x \rightarrow 0^+} f(x) =\lim_{x \rightarrow 0} (ax+b) = b
Para que haya límite, ambos límites laterales deben ser iguales, por tanto 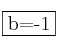\fbox{b=-1}

Veamos ahora en x=1
– f(1) = 2
– \lim_{x \rightarrow 1^-} f(x) =\lim_{x \rightarrow 1} (ax+b) = a+b
– \lim_{x \rightarrow 1^+} f(x) =\lim_{x \rightarrow 1} (2) = 2
Para que haya límite, ambos límites laterales deben ser iguales, por tanto a+b=2
Como b=-1, a-1=2 \longrightarrow \fbox{a=3}