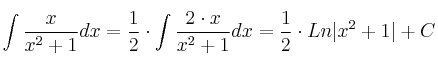Integrales Inmediatas
SOLUCIÓN
Es una integral inmediata de tipo Logaritmo Neperiano
Para aplicar la fórmula  necesitamos que en el numerador esté la derivada del denominador
necesitamos que en el numerador esté la derivada del denominador
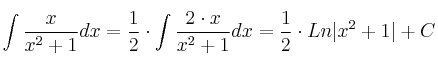
Es una integral inmediata de tipo Logaritmo Neperiano
Para aplicar la fórmula  necesitamos que en el numerador esté la derivada del denominador
necesitamos que en el numerador esté la derivada del denominador