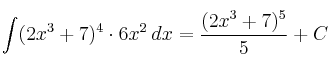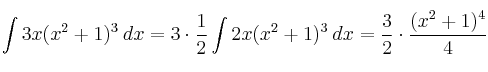Integrales Inmediatas. Potencia de una función
1 - Integrales Inmediatas
 Introducción a las Integrales
Introducción a las Integrales Integrales polinómicas. Primeras propiedades de las integrales
Integrales polinómicas. Primeras propiedades de las integrales Integrales Inmediatas. Potencia de una función
Integrales Inmediatas. Potencia de una función Integrales Inmediatas tipo Logaritmo Neperiano
Integrales Inmediatas tipo Logaritmo Neperiano Integrales Inmediatas tipo Exponencial
Integrales Inmediatas tipo Exponencial Integrales Inmediatas Trigonométricas tipo Sen-Cos
Integrales Inmediatas Trigonométricas tipo Sen-Cos Integrales Inmediatas tipo Tangente
Integrales Inmediatas tipo Tangente Integrales Inmediatas tipo arc sen y arc tg
Integrales Inmediatas tipo arc sen y arc tg Integrales Inmediatas. Resumen de Fórmulas
Integrales Inmediatas. Resumen de Fórmulas

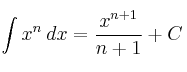 , tenemos la fórmula para una función elevada a un número:
, tenemos la fórmula para una función elevada a un número: