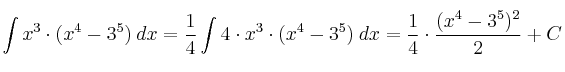Integrales Inmediatas del tipo d(u) · u
SOLUCIÓN
Se trata de dos integrales inmediatas del tipo "potencia de una función". Para resolverlas, aplicamos la fórmula:
![\int [u(x)]^n \cdot u’(x) \:dx = \frac{[u(x)]^{n+1}}{n+1} + C \int [u(x)]^n \cdot u’(x) \:dx = \frac{[u(x)]^{n+1}}{n+1} + C](local/cache-TeX/1846667d3a919b020bde8151bfccc46f.png?1688040057)
– 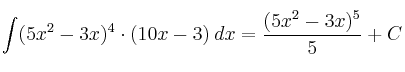
– 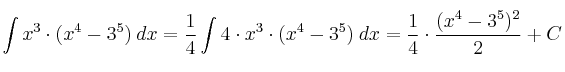
Se trata de dos integrales inmediatas del tipo "potencia de una función". Para resolverlas, aplicamos la fórmula:
![\int [u(x)]^n \cdot u’(x) \:dx = \frac{[u(x)]^{n+1}}{n+1} + C \int [u(x)]^n \cdot u’(x) \:dx = \frac{[u(x)]^{n+1}}{n+1} + C](local/cache-TeX/1846667d3a919b020bde8151bfccc46f.png?1688040057)
– 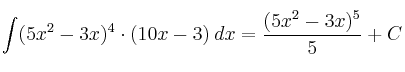
–