2006 - 2024 ► Matemáticas IES
©Daniel López Avellaneda, licenciado en Ciencias Matemáticas (Contactar)
Mapa del sitio
|
RSS 2.0
|
Privacidad
|
Cookies
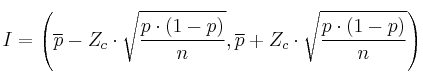
– ![]() : proporción de la población (cuando no se conozca se usará la de la muestra)
: proporción de la población (cuando no se conozca se usará la de la muestra)
– ![]() : proporción de la muestra
: proporción de la muestra
– ![]() : tamaño de la muestra
: tamaño de la muestra
– ![]() : valor crítico
: valor crítico
Cálculo del valor crítico ![]()
– Confianza: 90%, 95%, 98%, etc.
– Nivel de confianza: 0.90, 0.95, 0.98, etc.
– Significación+Confianza = 100%
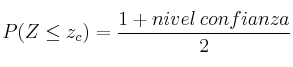
Ejemplo: Confianza del 95%
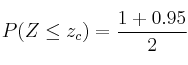
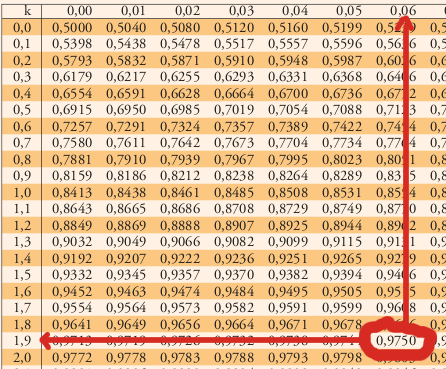
![]()
Miramos la tabla de la N(0,1) y obtenemos 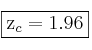
Definimos el máximo admisible como
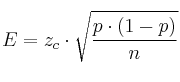
Lo habitual es que nos den el Error máximo y tengamos que calcular el tamaño mínimo de la muestra. De la fórmula anterior, despejamos ![]() y obtenemos:
y obtenemos:
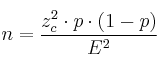
– El tamaño de la muestra debe ser como mínimo el siguiente nº entero al resultado obtenido con la fórmula anterior.
– Al aumentar el tamaño de la muestra disminuye el Error
2006 - 2024 ► Matemáticas IES
©Daniel López Avellaneda, licenciado en Ciencias Matemáticas (Contactar)
Mapa del sitio
|
RSS 2.0
|
Privacidad
|
Cookies

