Rectas tangente y normal a una curva
SOLUCIÓN
– a) La recta normal (perpendicular) a ![]() en
en ![]() tiene por ecuación
tiene por ecuación
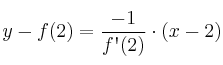
Por tanto la recta pedida es:
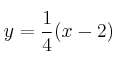
– b) La recta ![]() se puede expresar como
se puede expresar como 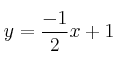 , por tanto su pendiente es
, por tanto su pendiente es ![]()
Dos rectas son perpendiculares cuando el producto de sus pendientes es ![]()
Si la pendiente de la recta pedida es ![]() , tenemos que
, tenemos que 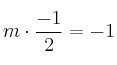 de donde
de donde ![]()
(1) Sabemos que la pendiente de la recta tangente vale ![]()
(2) Sabemos que la pendiente de la recta tangente es la derivada.
De (1) y (2) deducimos que ![]()
![]()
Por tanto, el punto que nos piden es el punto de abcisa 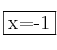 . La segunda coordenada del punto sería
. La segunda coordenada del punto sería ![]() , por consiguiente el punto es
, por consiguiente el punto es ![]()
