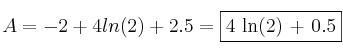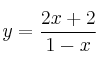Selectividad Andalucía 2001-2-B2

| 2 |

Halla el área del recinto rayado que aparece en la figura adjunta sabiendo que la parte curva tiene como ecuación y = \frac{2x+2}{1-x}

SOLUCIÓN

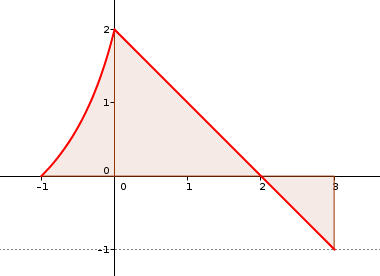
– El área del trozo bajo la parte curva sería:
\int_{-1}^0 \frac{2x+2}{1-x} dx

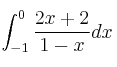
Se trata de una integral racional (Ver Teoría), por lo que debemos hacer el cociente de polinomios (2x+2) : (-x+1) y se obtiene (-2) de cociente y (4) de resto, con lo que podemos expresar la integral de la forma:

\int_{-1}^0 \frac{2x+2}{1-x} dx = \int_{-1}^0 -2 dx +\int_{-1}^0 \frac{4}{-x+1}dx=


=\left. -2x -4 ln|x-1| \right]_{-1}^0 = -2 + 4 ln(2)

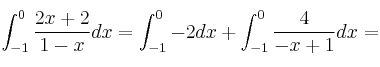
– El resto del área se puede calcular como la integral bajo la recta que pasa por los puntos (2,0) y (0,2). Habría que calcular la ecuación de la recta y después hacer una suma de integrales (una entre 0 y 2, y otra entre 2 y 3), teniendo en cuenta que la segunda integral habría que tomarla en valor absoluto (está bajo el eje).
Sin embargo, se puede hacer más fácil: como áreas de triángulos. Basta aplicar (base x altura)/2 y obtendríamos un área de 2 u^2 en el primer triángulo y de 0.5 u^2 en el segundo.

El área total que nos piden es:

A = -2 + 4 ln(2) + 2.5 = \fbox{4 ln(2) + 0.5}