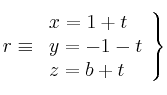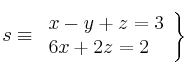a) Dos rectas están en el mismo plano cuando sean coincidentes, paralelas o secantes (es decir cuando no se cruzan). Si vemos la teoría de la posición relativa de 2 rectas en el plano Ver Vídeo, debemos crear una matriz formada por 3 vectores: un vector director de cada recta y un tercer vector formado por un punto de cada recta.
Como no se pueden cruzar, tiene que se rango(M)<3, es decir |M|=0
Por tanto, el procedimiento es calcular el determinante de la matriz e igualarlo a cero, y de ahí obtendremos el valor de
Un vector director de sería y un punto
De la recta , que viene en ecuación general o implícitas, obtenemos dos puntos y a partir de ellos un vector director. ¿Cómo obtener puntos de una recta en ec. general
Para se obtiene , Punto:
Para se obtiene , Punto:
De ambos puntos obtenemos un vector , pero podemos tomar uno proporcional para evitar fracciones (multiplicando por 3):

Ya podemos crear la matriz :
(vector director de r)
(vector director de s)
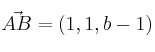(vector con un punto de cada recta)

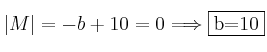
– b) El rango de M es 2 por lo que las rectas son secantes.
Para hallar la ecuación del plano que las contiene usamos un vector director de cada recta y un punto cualquiera de una de las rectas.
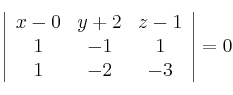