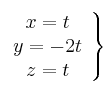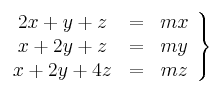Selectividad Andalucía 2008-6-A3
SOLUCIÓN
– a) Calculamos el determinante de la matriz de los coeficientes: ![]()
Igualamos a cero y resolvemos la ecuación:
![]()
![]()
![]() ;
; 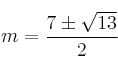
Cuando ![]() y
y 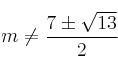 el det(A) será distinto de cero y entonces rg(A)=3 = rg(A*)=nº inc. (S.C.D.)
el det(A) será distinto de cero y entonces rg(A)=3 = rg(A*)=nº inc. (S.C.D.)
Para ![]() y para
y para 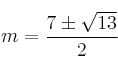 el sistema tiene infinitas soluciones pues rg(A)=2=rg(A*)<nºinc. (S.C.I.)
el sistema tiene infinitas soluciones pues rg(A)=2=rg(A*)<nºinc. (S.C.I.)
– b) Para ![]() es S.C.Det. con la única solución
es S.C.Det. con la única solución ![]()
Para ![]() es S.C. Indet. (infinitas soluciones). Las soluciones son:
es S.C. Indet. (infinitas soluciones). Las soluciones son: