Selectividad Andalucía 2013-2-A1

|

Sea R la región factible definida por las siguientes inecuaciones x \geq 3y , x \leq 5 , y \geq 1.

- a) (0.5 puntos) Razone si el punto (4.5, 1.55) pertenece a R.
- b) (1.5 puntos) Dada la función objetivo F(x,y)=2x-3y, calcule sus valores extremos en R.
- c) (0.5 puntos) Razone si hay algún punto de R donde la función F valga 3.5. ¿Y 7.5?

SOLUCIÓN

- a) Para que el punto (4.5, 1.55) pertenezca a R debe cumplir las 3 inecuaciones.
No cumple la inecuación x \geq 3y porque la relación 4.5 \geq 3 \cdot 1.55 es falsa. Por tanto no pertenece a R

- b) Dibujamos la región factible y calculamos sus vértices

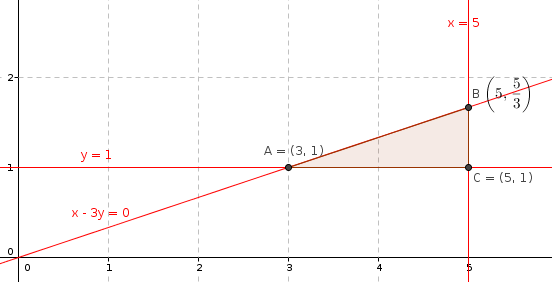
Aplicamos la función objetivo a cada uno de los vértices:
F(3,1)=2 \cdot 3 - 3 \cdot 1 =3
F(5,5/3)=2 \cdot 5 - 3 \cdot 5/3 =5
F(5,1)=2 \cdot 5 - 3 \cdot 1 = 7

Observamos que:
- El mínimo es 3 y lo alcanza en el punto (3,1)
- El máximo es 7 y lo alcanza en el punto (5,1)

- c) Si hay un punto en que la función valga 3.5 porque está entre los extremos: 3 \leq 3.5 \leq 7, pero no hay ningún punto donde la función valga 7.5 puesto que es mayor que el máximo (7).