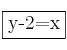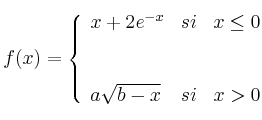Selectividad Andalucía 2013 - J - B1
SOLUCIÓN
– a) Como ![]() es derivable podemos expresar la derivada como
es derivable podemos expresar la derivada como
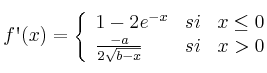
Al ser derivable en ![]() sus derivadas laterales serán iguales:
sus derivadas laterales serán iguales:
![]()
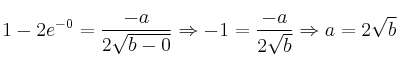
Por otra parte, como derivable implica continua, ![]() debe ser continua en
debe ser continua en ![]() , lo cual nos indica que:
, lo cual nos indica que:
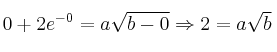
Resolviendo el sistema 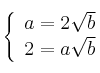 obtenemos
obtenemos 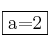 y
y 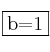
– b) Aplicamos las fórmulas de las rectas tangente y normal
![]() (recta tangente)
(recta tangente)
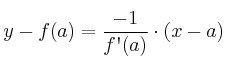 (recta normal)
(recta normal)
para ![]() y
y ![]() (el 0 está definido por el primer trozo)
(el 0 está definido por el primer trozo)
Obtenemos: 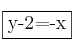 y
y