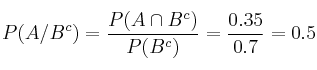Selectividad Andalucía 2014-1-A3
SOLUCIÓN
Datos que aporta el enunciado:
A y B son independientes
![]()
![]()
– a) Ay B independientes ![]()
![]()
![]() No son incompatibles
No son incompatibles
– b) ![]()
– c) 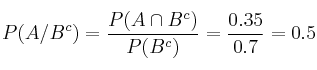
Datos que aporta el enunciado:
A y B son independientes
![]()
![]()
– a) Ay B independientes ![]()
![]()
![]() No son incompatibles
No son incompatibles
– b) ![]()
– c)