Selectividad Andalucía 2014-1-B3
SOLUCIÓN
Consideramos los sucesos:
E = "presentar defectos Eléctricos"
M = "presentar defectos Mecánicos"
El enunciado nos dice que:
![]()
![]()
![]()
– a) ![]()
Por otro lado
![]()
Por tanto ![]()
– b) 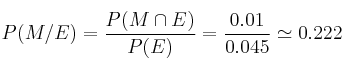
– c) ![]() No son incompatibles
No son incompatibles
![]() No son independientes
No son independientes
