Selectividad Andalucía 2014-2-A1
SOLUCIÓN
– a) Dibujamos las rectas, calculamos el semiplano solución para cada inecuación y obtenemos:
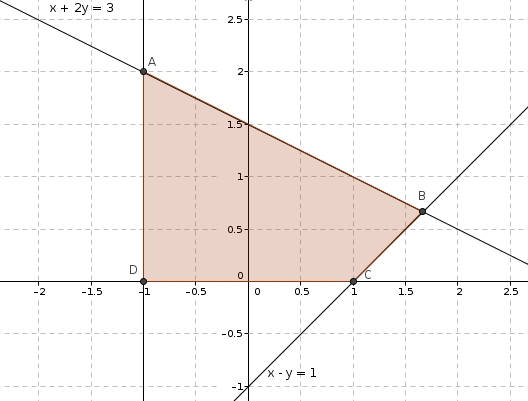
Para dibujar bien las rectas, es necesario tomar los puntos de corte con los ejes de coordenadas (hacemos x=0 y calculamos y; hacemos y=0 y calculamos x).
Si hemos dibujado bien las rectas, ya tendremos 3 de los vértices:
![]() ,
, ![]() y
y ![]()
Para calcular el vértice ![]() necesitamos resolver el sistema formado por las rectas
necesitamos resolver el sistema formado por las rectas ![]() y
y ![]() , que da como soluciones
, que da como soluciones 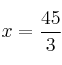 ;
; 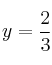 .
.
Por tanto los vértices son ![]() ,
,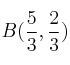 ,
, ![]() ,
, ![]()
– b) Aplicamos la función objetivo a todos los vértices:
![]()
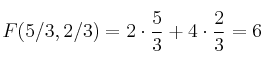
![]()
![]()
– Observamos que el máximo es ![]() y lo alcanza en los puntos
y lo alcanza en los puntos ![]() y
y ![]() (y por tanto en todos los puntos del segmento
(y por tanto en todos los puntos del segmento ![]()
– El valor mínimo es ![]() y lo alcanza en el punto
y lo alcanza en el punto ![]()
