Sistemas homogéneos

|

Sistemas Homogéneos

Decimos que un sistema de ecuaciones es homogéneo cuando todos los términos independientes son cero.

\left\{ \begin{array}{lll} a_{11}x + a_{12}y + a_{13}z = 0 \\ a_{21}x + a_{22}y + a_{23}z = 0 \\ a_{31}x + a_{32}y + a_{33}z = 0 \end{array} \right.

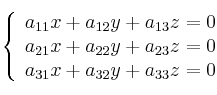
- Los sistemas homogéneos son siempre compatibles (SCD o SCI) puesto que la matriz de los coeficientes y la matriz ampliada tienen el mismo rango (al ampliar la matriz de los coeficientes con una file de ceros el rango no varía).

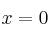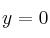- Cuando un sistema homogéneo sea Compatible Determinado (SCD), su solución única será la trivial: x=0 , y=0 , z=0