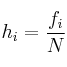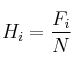Tablas estadísticas de frecuencias

|

Tabla de frecuencias para variables discretas

Los siguientes datos corresponden al número de hermanos en una clase de 20 alumnos:

3,1,1,2,3,4,3,2,5,2,2,3,4,2,1,4,2,3,1,2

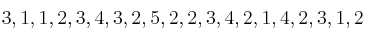
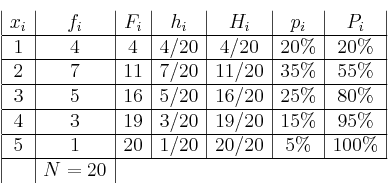
Con estos datos se crea la siguiente tabla:

\begin{array}{|c|c|c|c|c|c|c|} x_i & f_i & F_i & h_i & H_i & p_i & P_i \\ \hline 1 & 4 & 4 & 4/20& 4/20 & 20\% & 20\% \\ \hline 2 & 7 & 11 & 7/20& 11/20 & 35\% & 55\% \\ \hline 3 & 5 & 16 & 5/20& 16/20 & 25\% & 80\% \\ \hline 4 & 3 & 19 & 3/20& 19/20 & 15\% & 95\% \\ \hline 5 & 1 & 20 & 1/20& 20/20 & 5\% & 100\% \\ \hline & N=20 \\ \end{array}

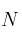– N : número total de datos
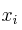– x_i : distintos valores de la variable o carácter estadístico objeto de estudio
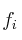– f_i : frecuencia absoluta (nº de veces que se repite cada valor)
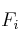– F_i : frecuencia absoluta acumulada. Consiste en sumar 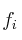f_i y todas las anteriores. Ejemplo: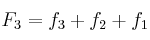 F_3=f_3+f_2+f_1
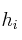– h_i : frecuencia relativa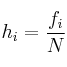 h_i=\frac{f_i}{N}
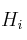– H_i : frecuencia relativa acumulada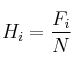 H_i=\frac{F_i}{N}
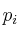– p_i : porcentaje (frecuencia relativa en porcentaje)
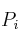– P_i : porcentaje acumulado

Crea una tabla con tus propios datos

Tabla de frecuencias para variables continuas

Cuando la variable es continua (puede tomar cualquier valor), los datos se agrupan en intervalos (a ser posible de la misma amplitud).

Veamos un ejemplo con estos datos:

38 32 54 47 50 58 46 61 43 54
47 55 60 43 60 45 48 52 40 30
40 53 59 48 39 48 56 34 44 62
52 48 55 60 53 43 52 48 51 52
46 55 56 54 48 39 50 51 52 39

Los agrupamos en intervalos de amplitud 10

\begin{array}{c|c|c|c|c|c|c|c|} & x_i & f_i & F_i & h_i & H_i & p_i & P_i \\ \hline [30,40) & 35 & 7 & 7 & 7/50& 7/50 & 14\% & 14\% \\ \hline [40,50) & 45 & 17 & 24 & 17/50& 24/50 & 34\% & 48\% \\ \hline [50,60) & 55 & 21 & 45 & 21/50& 45/50 & 42\% & 90\% \\ \hline [60,70) & 65 & 5 & 50 & 5/50& 50/50 & 10\% & 100\% \\ \hline & & N=50 \\ \end{array}

En este caso, los 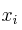x_i (marcas de clase) son los puntos medios de cada intervalo