inecuaciones grado1 1incógnita
SOLUCIÓN
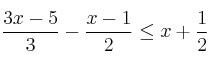
m.c.m.(3,2) = 6
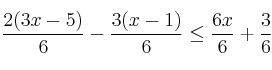
![]()
![]()
Debemos colocar las "x" de forma que queden positivas (lo hacemos en las inecuaciones; no sería necesario en las ecuaciones)
![]()
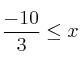
Podemos expresar la solución en forma de intervalo:
![]()
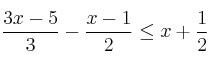
m.c.m.(3,2) = 6
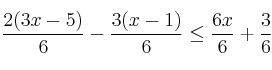
![]()
![]()
Debemos colocar las "x" de forma que queden positivas (lo hacemos en las inecuaciones; no sería necesario en las ecuaciones)
![]()
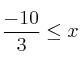
Podemos expresar la solución en forma de intervalo:
![]()