-
(#4615) - Selectividad Andalucía 2021-Julio-A1

Se considera la matriz
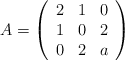
a) Determine para qué valores del parámetro
 , la matriz
, la matriz  tiene inversa.
tiene inversa.
b) Para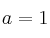 , calcule la inversa de
, calcule la inversa de  .
.
c) Para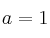 , resuelva la ecuación matricial
, resuelva la ecuación matricial 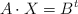 , siendo
, siendo 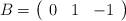
-
(#4614) - Selectividad Andalucía 2021-1-A2

Se consideran las matrices
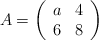
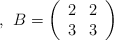 y
y 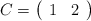
a) Calcule el valor del parámetro
 para que la matriz
para que la matriz  no tenga inversa.
no tenga inversa.
b) Para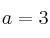 , resuelva la ecuación matricial
, resuelva la ecuación matricial 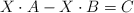 .
.
c) Para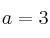 , compruebe que
, compruebe que 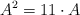 y exprese
y exprese 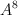
en función de la matriz .
. -
(#4005) - Selectividad Andalucía 2014-2-B1

– a) Determine los valores de x e y que hacen cierta la igualdad
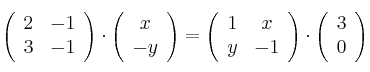
– b) Resuelva la ecuación matricial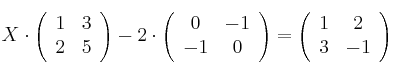
-
(#3905) - Selectividad Andalucía 2013-2-B1

Sean las matrices
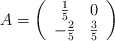
,
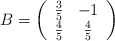
,
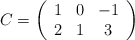
– a) Resuelva la ecuación matricial
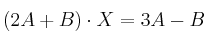
– b) Determine en cada caso la dimensión de la matriz D para que se puedan realizar las siguientes operaciones: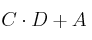 ,
, 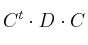 ,
, 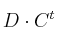 ,
, 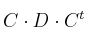
-
(#3300) - Selectividad Andalucía 2011-5-B1
Sean las matrices

a) Efectúe, si es posible, los siguientes productos:
– a1)
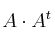
– a2)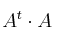
– a3)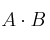
b) Resuelva la siguiente ecuación matricial
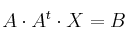
- 0
- 5
