Área bajo curva

|

Halla el área entre el eje de abcisas y la gráfica de la función f(x)=-x^2+2x+3 en el intervalo [1,4]

SOLUCIÓN

En primer lugar calculamos los puntos de corte con el eje de abcisas y a continuación dibujamos la función

x^2+2x+3=0
\begin{array}{ccc} & & x_1 = \frac{-2+4}{-2}=-1\\ & \nearrow &\\ x=\frac{-2\pm \sqrt{2^2-4 \cdot(-1)\cdot3}}{2 \cdot(-1)}= \frac{-2\pm \sqrt{16}}{-2}& &\\ & \searrow &\\& &x_2 = \frac{-2-4}{-2}=3\end{array}
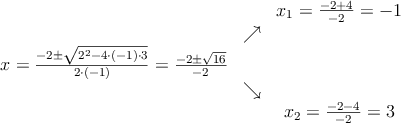
Uno de los cortes cae dentro del intervalo [1,4]

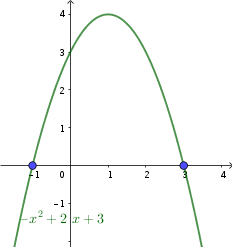
Debemos descomponerlo en una suma de integrales (y tomar valor absoluto, pues uno de los trozos cae debajo del eje)

A = \left| \int_1^3 (-x^2+2x+3)dx \right|+ \left| \int_3^4 (-x^2+2x+3)dx \right|

A =\left| \left[ \frac{-x^3}{3}+x^2+3x \right]_1^3 \right|+\left|\left[ \frac{-x^3}{3}+x^2+3x \right]_3^4 \right|=

A =\left| \left( \frac{-3^3}{3}+3^2+3 \cdot 3 \right) - \left( \frac{-1^3}{3}+1^2+3 \cdot 1 \right) \right|+

\left|\left( \frac{-4^3}{3}+4^2+3 \cdot 4 \right) - \left( \frac{-3^3}{3}+3^2+3 \cdot 3 \right) \right| =

\left| 9-\frac{11}{3} \right| + \left| \frac{20}{3}-9 \right| = \frac{16}{3}+\frac{7}{3}=\textcolor{blue}{\frac{23}{3} \: u^2}