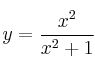Funciones Extremos Relativos

Halla los extremos relativos de la función $y=\frac{x^2}{x^2+1}$

SOLUCIÓN

$f(x)=\frac{x^2}{x^2+1}$

$f^\prime(x)=\frac{2x \cdot (x^2+1) - x^2 \cdot 2x}{(x^2+1)^2}=\frac{2x^3+2x-2x^3}{(x^2+1)^2} = \frac{2x}{(x^2+1)^2}$

$f^\prime(x)=0 \longrightarrow \frac{2x}{(x^2+1)^2}=0 \longrightarrow 2x=0 \longrightarrow x=0$

El punto es el único candidato a Máximo o Mínimo.

Para ver si es máximo o mínimo podemos usar la segunda derivada como en Extremos de una función

Otra opción es estudiar la monotonía y aprovechar que la función es continua.

Lo vamos a hacer con el método de la segunda derivada

$f^\prime(x)=\frac{2x}{(x^2+1)^2}$

$f^{\prime\prime}(x)=\frac{2 \cdot (x^2+1)^2 - 2x \cdot 2 \cdot (x^2+1) \cdot 2x}{(x^2+1)^4}$

$f^{\prime\prime}(x)=\frac{2 \cdot (x^2+1)^2 - 8x^2 \cdot (x^2+1)}{(x^2+1)^4}$

No es necesario simplificar puesto que la tenemos que aplicar a y los cálculos no son complicados

$f^{\prime\prime}(0)=\frac{2 \cdot (0^2+1)^2 - 8 \cdot 0^2 \cdot (0^2+1)}{(0^2+1)^4} = 2 > 0 \longrightarrow$ en hay un MÍNIMO

Calculamos la 2ª coordenada en la función original
$f(0)=\frac{0^2}{0^2+1}=0$

Por tanto el MÍNIMO es

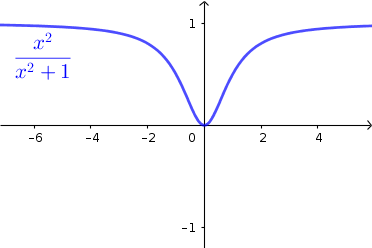
Aunque no lo pide el ejercicio, voy a dibujar la gráfica para comprobar el resultado