Interés compuesto

|

Contratamos un depósito al 2% con aportaciones trimestrales. Al cabo de 5 años obtenemos un capital final de 7346.13 euros.
Calcula el capital inicial que se depositó y los intereses totales que ha producido en esos 5 años. Calcula la tasa anual equivalente (TAE) correspondiente.

SOLUCIÓN

Como los pagos son trimestrales, usaremos la fórmula del interés compuesto Ver Teoría donde t son trimestres:
C = c \cdot \left( 1 + \frac{r}{400} \right)^t
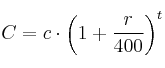
Sustituimos en la fórmula los datos del enunciado (5 años son 20 trimestres)
7346.13 = c \cdot \left( 1 + \frac{2}{400} \right)^{20}
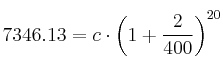
Tenemos que calcular el capital inicial (c)
7346.13 = c \cdot \left( 1.005 \right)^{20}

\frac{7346.13}{\left( 1.005 \right)^{20}} = c
6648.71 = c

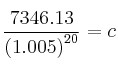
Se depositó un capital inicial de 6648.71€ y se obtuvo un capital final de 7346.13€, por tanto, los intereses generados han sido de 697.42 €

Usaremos la fórmula para el cálculo de la TAE:
TAE = \left( 1 + \frac{i}{k} \right)^k -1
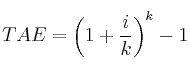
Recordemos que k es el número de veces al año. Como son pagos trimestrales sería 4 veces al año

TAE = \left( 1 + \frac{0.02}{4} \right)^4 -1 = 0.020150501
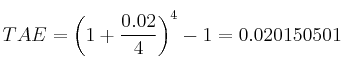
Sería una TAE del 2.02%