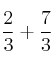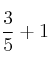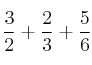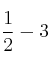Publicar un mensaje
En respuesta a:
fracciones operaciones
SOLUCIÓN
apartado a)
![]()
Como tienen igual denominador, basta con operar con los numeradores
![]()
– apartado b)
![]()
Como tienen distinto denominador, debemos reducirlas a común denominador (calculando el mínimo común múltiplo de los denominadores)
![]()
dividimos 5 entre el denominador y multiplicamos por el numerador
![]()
– apartado c)
![]()
Como tienen distinto denominador, debemos reducirlas a común denominador (calculando el mínimo común múltiplo de los denominadores)
![]()
dividimos 12 entre el denominador y multiplicamos por el numerador
![]()
![]()
![]()
– apartado d)
![]()
dividimos 2 entre el denominador y multiplicamos por el numerador
![]()