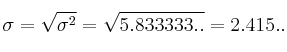SOLUCIÓN

Al sumar los puntos de dos datos obtendremos unos valores que oscilan entre 2 (1+1) y 12 (6+6). Para expresar la tabla de probabilidades, basta con asignar probabilidades a los diferentes valores (2 a 12) de la variable.
Por ejemplo, para que la suma sea 3 tenemos 2 opciones (1+2 , 2+1) de los 36 sucesos elementales que componen el espacio muestral de lanzar 2 dados.

– b)

– c)