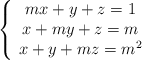Discutir sistema en función de parámetro 4624
SOLUCIÓN
Expresamos la matriz de los coeficientes y la matriz ampliada
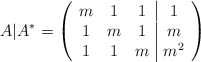
Estudiamos el rango de ambas matrices en función de m. Para ello empezamos calculando |A|
![]()
Veamos cuando el determinante vale cero.
![]()
![\polyhornerscheme[x=1,resultstyle=\color{red},resultbottomrule,resultleftrule,resultrightrule]{x^3-3x+2} \polyhornerscheme[x=1,resultstyle=\color{red},resultbottomrule,resultleftrule,resultrightrule]{x^3-3x+2}](local/cache-vignettes/L185xH82/73952f10de4a79b1bb05bf575e3f10a5-65b37.png?1700510563)
![\polyhornerscheme[x=1,resultstyle=\color{red},resultbottomrule,resultleftrule,resultrightrule]{x^2+x-2} \polyhornerscheme[x=1,resultstyle=\color{red},resultbottomrule,resultleftrule,resultrightrule]{x^2+x-2}](local/cache-vignettes/L143xH82/ebf9fa2c1693956623742ebc708275d4-d56e3.png?1700510563)
![\polyhornerscheme[x=-2,resultstyle=\color{red},resultbottomrule,resultleftrule,resultrightrule]{x+2} \polyhornerscheme[x=-2,resultstyle=\color{red},resultbottomrule,resultleftrule,resultrightrule]{x+2}](local/cache-vignettes/L118xH82/b40d3f049479fce48caf9570ca2b2b74-de6ca.png?1688048373)
– Si ![]() y
y ![]()
Como ![]() y número de incógnita es también 3, por el Teorema de Rouché tenemos un S.C.D. (Sistema Compatible Determinado)
y número de incógnita es también 3, por el Teorema de Rouché tenemos un S.C.D. (Sistema Compatible Determinado)
– Si ![]() veamos como quedan las matrices
veamos como quedan las matrices
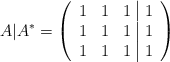
Se ve claramente que ![]()
Ambos rangos son iguales y menores al nº de incógnitas. El teorema de Rouché nos dice que es un S.C.I. (Sistema Compatible Indeterminado), cuya solución sería la siguiente:
![]()
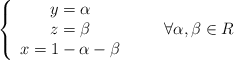
– Si ![]() quedaría
quedaría
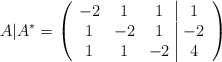
Calculamos el rango de A
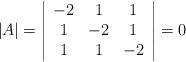
(Ya sabíamos que para m=-2 |A|=0). No hacía falta calcularlo.
![]()
Veamos ahora el rango de la ampliada
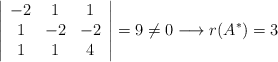
Como tienen rangos distintos, se trata de un S.I. (Sistema Incompatible) según el teorema de Rouché.