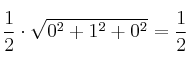Ejercicio vectores en el espacio
SOLUCIÓN
Preparamos los vectores que necesitaremos en los siguientes apartados:
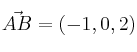 ,
, 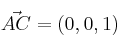 ,
, 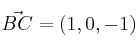
– a) 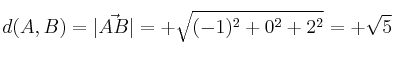
– b) 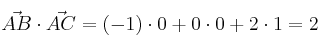
– c) Perímetro = ![]()
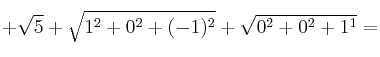
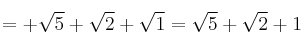
– d) Calculamos el área del triángulo con la fórmula:
Área = 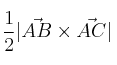
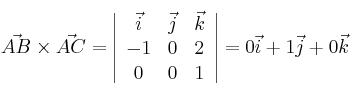
Por tanto, Área = 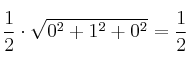
Preparamos los vectores que necesitaremos en los siguientes apartados:
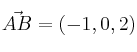 ,
, 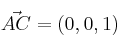 ,
, 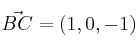
– a) 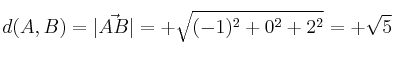
– b) 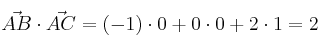
– c) Perímetro = ![]()
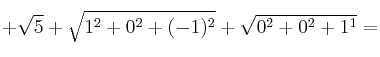
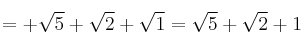
– d) Calculamos el área del triángulo con la fórmula:
Área = 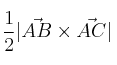
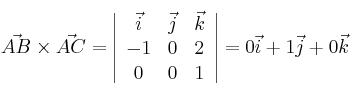
Por tanto, Área =