SOLUCIÓN

– a) es una función polinómica, por tanto su dominio es (todos los números reales).
La función 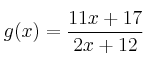es racional, por tanto su dominio es todos los números reales excepto los que anulan el denominador ()

– b) Puntos de corte de
Si . Punto
Si . Ecuación de segundo grado que tiene como soluciones ; . Puntos y

Puntos de corte de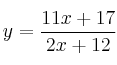
Si 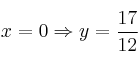. Punto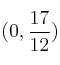
Si 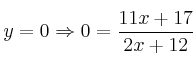. Resolvemos la Ecuación y obtenemos como solución 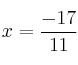. Punto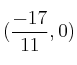

– c) es una función polinómica de segundo grado, por tanto su gráfica es una parábola.
Para dibujar la parábola calculamos vértice, orientación, corte con los ejes (hecho en el apartado anterior) y, si es necesario, algunos puntos más.

Vértice: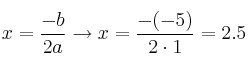

Por tanto el vértice es

Orientación: la parábola va hacia arriba (convexa) por ser positivo el coeficiente de

Corte con los ejes: , y

Otros puntos
Si , . Punto
Por simetría podemos obtener más puntos: ,

Con todos los datos anteriores ya podemos dibujar la parábola

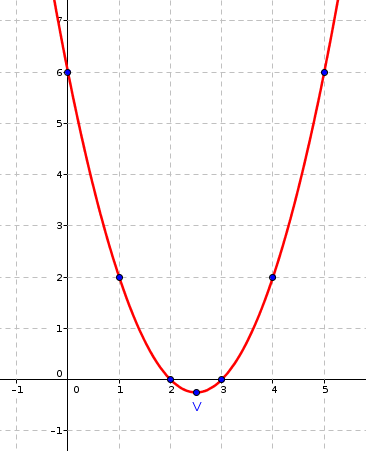
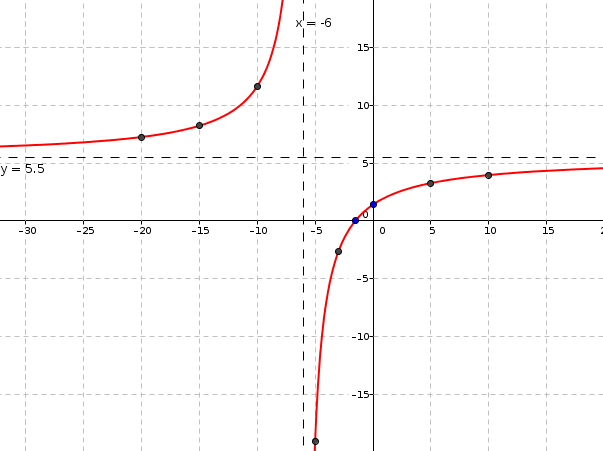
La función 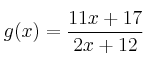es una hipérbola. Para dibujarla basta con calcular sus asíntotas y obtener algunos puntos auxiliares
Asíntota horizontal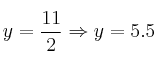
Asíntota vertical