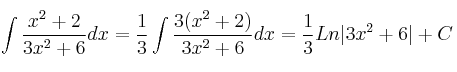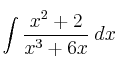Integral resuelta de dos formas: inmediata y sustitución

|

Resuelve la intergral \int \frac{x^2+2}{x^3+6x} \: dx

SOLUCIÓN

Otra forma de resolver la integral es de forma directa, es decir es una integral casi inmediata de tipo Ln |f(x)| porque el numerador es casi la derivada del denominador

La derivada del denominador es (x^3+6x)’ = 3x^2+6 = 3 \cdot (x^2+2)

Necesitaríamos un 3 multiplicando, podemos ponerlo a cambio de multiplicar también por \frac{1}{3} par que la expresión no cambie.

Como resultado obtendríamos:
\int \frac{x^2+2}{3x^2+6} dx = \frac{1}{3}\int \frac{3(x^2+2)}{3x^2+6} dx = \frac{1}{3} Ln|3x^2+6| + C