Problema de optimización
SOLUCIÓN

– En primer lugar hacemos el dibujo y asignamos incógnitas a los datos desconocidos.
– Escribimos la función a optimizar (maximizar o minimizar): en nuestro caso es el volumen, que debemos maximizar
Volumen ![]()
– La función a maximizar (el volumen) debe tener una sola variable. Como en nuestro caso tiene 2 variables ( x, y), debemos buscar alguna relación entra ambas para conseguir que haya una sola variable.
– La relación (entre x e y) que buscamos, suele venir en los datos del problema.
– El problema dice que el área vale 300 (la suma de el suelo y las 4 paredes).
![]()
La expresión anterior relaciona ![]() e
e ![]() . Ahora debemos despejar una de ellas en función de la otra (y después sustituir su valor en la función a maximizar).
. Ahora debemos despejar una de ellas en función de la otra (y después sustituir su valor en la función a maximizar).
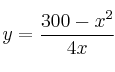
– Expresamos el volumen como ![]()
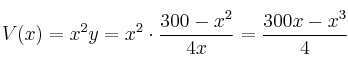
– Una vez que tenemos la función a maximizar con una sola variable, solo nos queda buscarle los extremos (máximo en este caso).
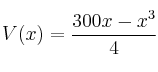
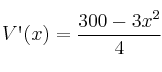
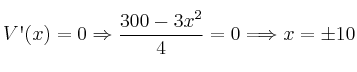
A las 2 soluciones ![]() , candidatos a extremos, le aplicamos la segunda derivada para comprobar si alguno de ellas es máximo.
, candidatos a extremos, le aplicamos la segunda derivada para comprobar si alguno de ellas es máximo.
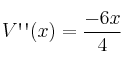
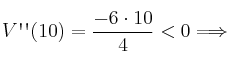 MAX en
MAX en ![]()
Por tanto, las dimensiones son ![]() e
e 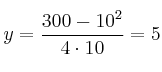
La caja debe tener ![]() de base y
de base y ![]() de altura
de altura
