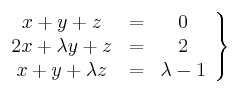Selectividad Andalucía 2007-3-B3
SOLUCIÓN
– a) Expresamos la matriz de los coeficientes (A) y la matriz ampliada (A*)
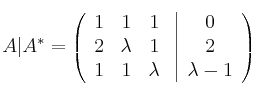
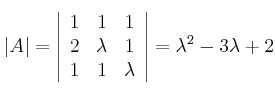
![]()
– Si ![]() y
y ![]()
Como ![]() y nº incógnitas=3, según el teorema de Rouché, el Sistema es Compatible Determinaddo.
y nº incógnitas=3, según el teorema de Rouché, el Sistema es Compatible Determinaddo.
– Si ![]() , las matrices serían
, las matrices serían
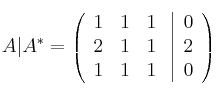
Ya sabemos que para ![]() el det(A)=0 (el rango de A no puede ser 3). Veamos si el rango de A vale 2:
el det(A)=0 (el rango de A no puede ser 3). Veamos si el rango de A vale 2:
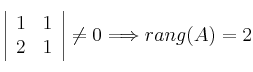
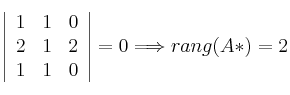
Se trata de un Sistema Compatible Indeterminado
– Si ![]() , las matrices serían
, las matrices serían
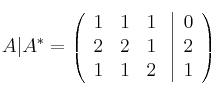
Ya sabemos que para ![]() el det(A)=0 (el rango de A no puede ser 3). Veamos si el rango de A vale 2:
el det(A)=0 (el rango de A no puede ser 3). Veamos si el rango de A vale 2:
Tomamos las filas 1 y 2; columnas 2 y 3
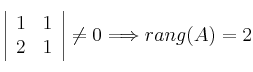
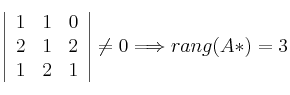
Se trata de un Sistema Incompatible
Por tanto Sist. Incomp. para ![]()
– b) Resolvemos el sistema para ![]() (en el apartado anterior hemos visto que es Compatible Indeterminado para
(en el apartado anterior hemos visto que es Compatible Indeterminado para ![]() ).
).
Las matrices son 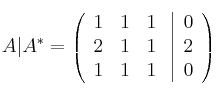
El determinante que daba el rango a la matriz A, era el formado tomando las 2 primeras filas y las dos primeras columnas 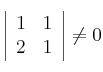 , por tanto eliminamos la 3ª fila y pasamos la 3ª columna a los términos independientes, quedando:
, por tanto eliminamos la 3ª fila y pasamos la 3ª columna a los términos independientes, quedando:
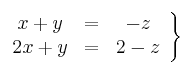
Haciendo ![]() y resolviendo el sistema 2x2 obtenemos las soluciones:
y resolviendo el sistema 2x2 obtenemos las soluciones:
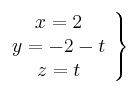 (con
(con ![]() )
)