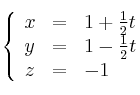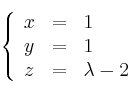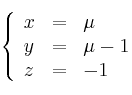Selectividad Andalucía 2009-3-A4
SOLUCIÓN
Usaremos el procedimiento descrito en este vídeo
Necesitamos un punto genérico y un vector director de cada recta (es fácil obtenerlos puesto que ambas rectas vienen en ecuaciones paramétricas)
Recta r :
– punto genérico ![]()
– vector ![]()
Recta s :
– punto genérico ![]()
– vector ![]()
Construimos el vector 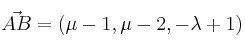
Aplicamos el procedimiento: el vector ![]() debe ser perpendicular a los vectores
debe ser perpendicular a los vectores ![]() y
y ![]()
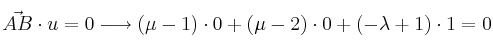
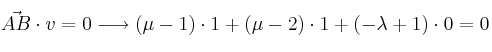
Operamos y simplificamos ambas ecuaciones, quedando
![]()
![]()
Por tanto, ![]() y
y ![]()
Los puntos A y B don entonces ![]() y
y ![]()
Con los puntos ![]() y
y ![]() construimos la ecuación de la recta pedida: tomamos como punto
construimos la ecuación de la recta pedida: tomamos como punto ![]() y como vector
y como vector 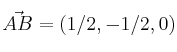
La recta, en paramétricas es: