Selectividad Andalucía 2011-5-A3
SOLUCIÓN
Para resolver el ejercicio necesitamos recordar la propiedad ![]()
– a) 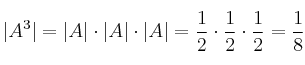
– b) Sabemos que ![]() . Por otra parte,
. Por otra parte, ![]() . Entonces:
. Entonces:
![]()
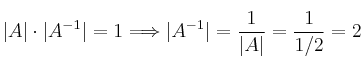
– c) 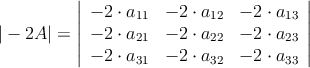
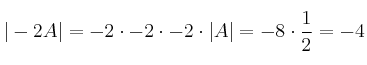
– d) 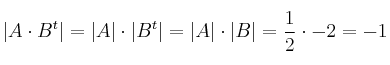
(Recordemos que el determinante de una matriz y el de su traspuesta son iguales)
– e) ![]()

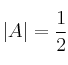 y
y