Selectividad Andalucía 2012-2-B4
SOLUCIÓN
Se trata de un contraste de hipótesis para proporción de tipo unilateral (Ver Teoría)
Contraste
![]() (hipótesis nula)
(hipótesis nula)
![]() (hipótesis alternativa)
(hipótesis alternativa)
Región de aceptación (R)
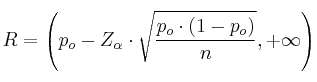
– ![]()
– ![]() (tamaño de la muestra)
(tamaño de la muestra)
– 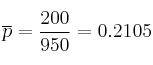 (proporción de la muestra)
(proporción de la muestra)
– ![]() al
al ![]()
![]()
Miramos la tabla de la N(0,1) y vemos que los mas próximo a 0.95 es 0.9495 (1.64) y 0.9505(1.65). Tanto si tomamos 1.64, como si tomamos 1.65 nos deberían dar el resultado por bueno, no obstante, como está a la misma distancia de ambos, voy a tomar 1.645 (la mitad entre 1.64 y 1.65).
Por tanto ![]()
La región de aceptación sería:
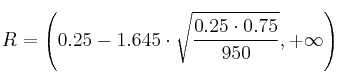
![]()
Como la proporción de la muestra está fuera de la región de aceptación ![]() , rechazamos la hipótesis nula (
, rechazamos la hipótesis nula (![]() ) de que al menos el
) de que al menos el ![]() de los usuarios de teléfonos móviles son de
de los usuarios de teléfonos móviles son de
contrato y admitimos que la proporción de personas con contrato en su teléfono móvil ha disminuido
